2024. 11. 17. 13:07ㆍ스터디/24-2 스터디 _ 밑바닥부터 시작하는 딥러닝
신경망을 구성하는 층(계층) 각각을 클래스 하나로 구현
활성화 함수(ReLU, Sigmoid) 계층 구현
5.5.1 ReLU 계층
-ReLU 수식

- ReLU 미분

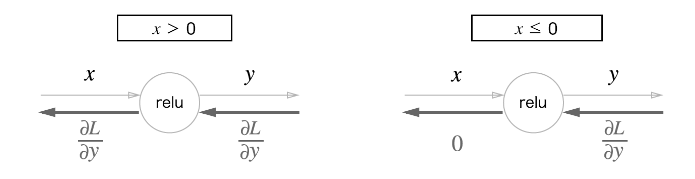
(순전파 때의 입력 x) >0 : 역전파는 상류의 값을 그대로 하류로 흘림(=1을 보냄)
(순전파 때의 입력 x) <=0 : 역전파 때는 하류로 신호를 보내지 않음(=0을 보냄)
-ReLU 계층의 계산 그래프
: 전자는 1을 보내고(그대로 보내고), 후자는 0을 보낸다.(신호를 보내지 않는다.)
-ReLU 계층 구현 -코드
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx값이 0 이하인 원소들은 모두 0으로 변경함.
값이 0 초과인 원소들은 그대로 유지함.
-def forward(self, x) 세부
self.mask = (x <= 0)배열의 각 원소가 0 이하이면 TRUE, 0 초과 이면 FALSE 인 배열을 self .mask에 저장
self .mask의 배열은 TRUE 또는 FALSE 중 한 개로 나타내지는 원소들로 구성됨
out = x.copy()x 배열의 복사본을 out에 저장
그러므로 out을 수정하더라도 원본인 x에는 영향을 주지 않음
out[self.mask] = 0self .mask에서 TRUE인 원소들을 모두 0으로 바꿈
-IF 순전파 때의 입력 값 <= 0, 역전파 때의 값=0
-> 역전파 시, 순전파 때의 mask 써서 원소가 TRUE 인 곳에서는 상류에서 전파된 dout를 0으로 설정함
5.5.2 Sigmoid 계층
-Sigmoid 수식
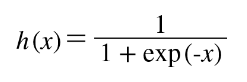
-Sigmoid 계층의 계산 그래프(순전파)

-'exp' 노드 : y=exp(x) 계산 수행
-'/' 노드 : y=1/x 계산 수행
-Sigmoid 계층의 계산 그래프(역전파)
1단계) '/' 노드
- 상류에서 흘러온 값 * -y^2(순전파의 출력 제곱 후 마이너스 붙인 값) 를 하류로 전달


2단계) '+' 노드
- 상류의 값을 그대로 하류로 전달

3단계) 'exp' 노드
- 상류의 값 * 순전파 때의 출력 을 하류로 전달

y=exp(x) 연산 수행함

4단계) 'x' 노드
- 순전파 때의 값을 '서로 바꿔' 곱한 후 하류로 전달


-역전파의 최종 출력인 이 값이 하류 노드로 전파됨
-순전파의 입력 x와 출력 y만으로 계산 가능
--> 계산 그래프의 중간 과정을 모두 묶어 'Sigmoid' 노드 하나로 대체 가능


-Sigmoid 계층의 역전파는 순전파의 출력(y)만으로 계산할 수 있음(x 없이도 가능함)
-->

-Sigmoid 계층 구현- 코드
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out # (1-y)*y
return dx(1.0 - self.out) * self.out = (1-y)*y
순전파의 출력을 out(인스턴스 변수)에 보관했다가, 역전파 계산 때 그 값을 사용함
'스터디 > 24-2 스터디 _ 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| 6.5 적절한 하이퍼파라미터 값 찾기 (0) | 2024.11.24 |
|---|---|
| 5.6 Affine/Softmax 계층 구현하기 + 5.7 오차역전파법 구현하기 (0) | 2024.11.17 |
| 4.6 정리 (0) | 2024.11.10 |
| 4.2 손실 함수 (0) | 2024.11.10 |
| 3.2 활성화 함수 (0) | 2024.11.03 |