2024. 11. 3. 17:26ㆍ스터디/24-2 스터디 _ 밑바닥부터 시작하는 딥러닝
3.2.1 시그모이드 함수(sigmoid function)
-신경망에서 사용하는 활성화 함수
-S자 모양 함수

-신경망에서의 이용 : 신호 변환 -> 변환된 신호를 다음 뉴런으로 전달
3.2.2 계단 함수 구현하기
-계단 함수 : 임계값을 경계로 출력이 바뀌는 함수.
-계단 함수 구현 방법 1
def step_function(x):
if x > 0:
return 1
else:
return 0
*입력이 0을 넘으면 1을 출력하고 그 외에는 0을 출력함
*인수로는 실수(부동소수점)만 가능(넘파이 배열 불가능)
-계단 함수 구현 방법 2
def step_function(x):
y = x > 0:
return y.astype(np.int)
>>> import numpy as np
>>> x = np.array([-1.0, 1.0, 2.0]) #넘파이 배열
>>> x
array([-1., 1., 2.])
>>> y = x > 0
>>> y
array([False, True, True], dtype=bool)
>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])
*넘파이 배열도 지원되도록
*astype() 메서드 : 넘파이 자료형 변환 / 원하는 자료형을 인수로 지정
3.2.3 계단 함수의 그래프
-0을 경계로 출력이 0에서 1로(또는 1에서 0으로) 바뀜 -> 값이 바뀌는 형태가 계단처럼 생김

3.2.4 시그모이드 함수 구현하기
def sigmoid(x):
return 1 / (1 + np.exp(-x))
* np.exp(-x) = exp(-x) = e^-x
-시그모이드 함수에서는, 인수로 넘파이 배열도 가능함
-넘파이 배열의 처리 : 브로드캐스트 기능
-그래프

3.2.5 시그모이드 함수와 계단 함수 비교

-차이점 : 출력
| 계단 함수 | 시그모이드 함수 |
| 0을 경계로 갑자기 출력 변화 0과 1 중 하나의 값만을 돌려줌 (퍼셉트론에서는 0 혹은 1만 흐른다) |
입력에 따라 출력이 연속적으로 변화 실수를 돌려줌 (신경망에서는 연속적 실수가 흐른다) |
-공통점 1 : 동일한 모양(구조)
*입력 작을 때는 0에 가깝고(혹은 0이고) 입력 클 때는 1에 가깝다.(혹은 1이다.)
*입력이 중요하면 큰 값 출력, 입력이 중요하지 않으면 작은 값 출력
*입력이 아무리 작거나 커도 출력은 반드시 0과 1 사이
3.2.6 비선형 함수
-공통점 2 : 비선형 함수
[비선형 함수 : '선형이 아닌' 함수.
직선 1개로는 그릴 수 없는 함수.
직선 2개 이상으로 구성되거나 곡선으로 구성된 함수]
*시그모이드 함수 : 곡선
계단 함수 : 구부러진 직선
-신경망에서는 활성화 함수로 비선형 함수를 사용해야만 한다.(선형 함수 사용 불가)
-이유 : 선형 함수를 사용하면 신경망의 층을 깊게하는 의미가 없어짐
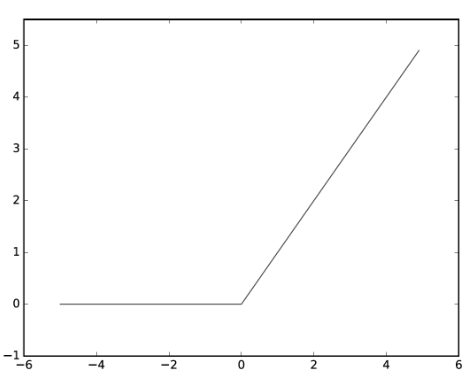
3.2.7 ReLU 함수(Rectified Linear Unit)
-활성화 함수의 일종
-입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 0을 출력하는 함수
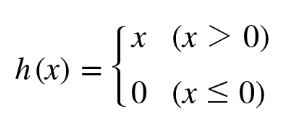
-ReLU 함수 구현 코드
def relu(x):
return np.maximum(0, x)
#maximum 함수 : 두 입력 중 큰 값을 선택해 반환하는 함수
'스터디 > 24-2 스터디 _ 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| 6.5 적절한 하이퍼파라미터 값 찾기 (0) | 2024.11.24 |
|---|---|
| 5.6 Affine/Softmax 계층 구현하기 + 5.7 오차역전파법 구현하기 (0) | 2024.11.17 |
| 5.5 활성화 함수 계층 구현하기 (0) | 2024.11.17 |
| 4.6 정리 (0) | 2024.11.10 |
| 4.2 손실 함수 (0) | 2024.11.10 |